LF精炼作为冶炼高品质钢的标准化工序之一,在钢厂得到了大规模应用。为了提高精炼效果和生产效率,偏心底吹成为了LF精炼常用的底吹模式,但是该底吹模式在促进精炼效果的同时会使钢包炉衬受到不均匀的壁面剪切力,即离透气砖较近的炉衬受到的壁面剪切力较大,对此处耐火材料形成了严重的流动冲刷。此外,高温条件下LF精炼渣会对钢包渣线处镁碳砖造成化学侵蚀,同时热流体的冲刷会加速化学侵蚀,导致渣线部分镁碳砖的熔损破坏是钢包炉衬中最为严重的。因此,渣线处炉衬耐火材料的熔损破坏程度直接决定了钢包是否需要离线大修,为了明确钢包大修周期,保证生产顺利进行,降低生产成本,生产现场必需对渣线处炉衬耐火材料的熔损破坏程度进行预先判断。目前,对渣线处炉衬剩余厚度的检测方法有直接测量法和数值模拟法两类。直接测量法包括激光法,超声波法和红外测温法。激光法首先使用定位激光确定钢包位置定位坐标,而后使用测量激光对钢包内壁面进行扫描,获取空间距离,再将所得数据转换为钢包壁面厚度。该方法测量精度高,坐标定位不确定度小于等于3.0 mm,但在钢包热修阶段需额外布置定位激光与扫描激光发射器,对生产节奏存在一定影响。超声波在金属材料和非金属材料中传播速度具备较大的差异,因此超声波法可用于炉壁厚度检测,但也需在测量点位布置超声波发生器与接收器,对精炼车间设备与人员配置提出了一定要求。红外测温法是目前应用最为广泛的钢包厚度检测方法,其操作便捷,可在钢包热修时由车间人员手动测量,也可由红外摄像仪进行远程测量,测得点、面温度后,求解导热微分方程得到钢包壁面厚度,但由于测得温度误差及钢包不同位置接触热阻的不均匀性,导致计算结果精准度存在较大误差。除直接测量外,有学者通过数值模拟对钢包炉衬熔损情况进行了预测,结合流动传热计算结果,将炉衬热应力分布加载到疲劳分析中,预测炉衬厚度的变化,但是该方法对几何建模和材料物性参数准确度要求高,无法及时响应现场需求。此外,目前所建立的数值模型中仅考虑了炉衬受到的冲刷磨损,忽略了熔渣造成的化学侵蚀。在满足不对生产节奏造成显著影响,尽可能减少操作人员工作量且具备一定预测精度的三个前提下,本文就国内某钢厂精炼钢包离线大修时间存在较大误差的问题提出了解决方案,该方案首先通过机理分析得出了影响精炼钢包耐火材料磨损的参数,而后与现场记录参数取交集,从而确定神经网络的输入参数,而后根据钢包精炼参数与大修记录参数之间多对一的特点,修改了神经网络的参数更新时间,实现了钢包渣线处剩余耐火材料厚度预测。同时为了缩短模型预测时间,提高预测精度,本文还对比了不同的隐藏层数量、学习率、激活函数以及神经网络类型等对模型预测结果的影响。
1 钢包蚀损预测模型
1.1 蚀损分析及假设
图1记录了某钢厂多次钢包大修时渣线处不同位置炉衬的剩余厚度。该230t双透气砖底吹钢包炉衬初始厚度为200 mm,大修时不同位置剩余耐材厚度呈现出了明显的不均匀性,可以看到,P2和P4两个位置炉衬的蚀损比P1和P3两个位置炉衬的蚀损更严重,而且即使在同一位置,不同大修时检测到的炉衬剩余厚度也存在较大波动,如P2位置最大剩余耐材厚度与最小剩余耐材厚度相差约50 mm,占初始厚度的四分之一,这表明目前的测量方法存在较大误差。(a)渣线处炉衬厚度测量点方位;(b)大修时渣线处不同位置炉衬剩余厚度。渣线处炉衬蚀损严重是LF精炼炉的一大特征[20,21],该处炉衬所处环境复杂,高温下与熔渣和钢水同时发生动态接触。精炼过程中镁碳砖内的碳会被氧化逃逸,熔渣也会沿着孔隙进入耐火材料内部,与镁砂反应形成侵蚀层,而侵蚀层与镁碳砖的物理性质并不一致,经历热流体冲刷后容易剥落进入钢水中形成大尺寸外来夹杂,对钢水质量造成了严重的负面影响。渣线处炉衬蚀损的不均匀性是双透气砖等流量偏心底吹导致的,该种吹氩方式会造成渣眼近壁面处渣层较薄,远壁面处渣层较厚,不同的渣层厚度耦合非均匀的流动传热增加了炉衬蚀损现象的复杂多变性。由上述分析可知,影响渣线处炉衬蚀损的因素有:流场,温度分布,以及熔渣、钢水和耐火材料的性质等。钢水的温度影响着产品质量,诸多学者建立了高精度的预测模型来监测温度变化,在数据记录中体现为钢水的入站和出站温度。流场在记录中则体现为钢包的几何尺寸、透气砖位置、氩气吹入量与持续时间等。在本研究中,钢包结构,透气砖位置,渣系、钢水和镁碳砖成分等均保持不变,因此,暂时忽略这些因素对炉衬蚀损行为的影响。本文利用LF处理时间、通电时间、通电量、吹氩时间、吹氩量、石灰加入量和钢水出站温度等7个工艺参数来训练神经网络,建立预测模型。
1.2 预测模型采用的神经网络
1.2.1 BP神经网络
BP神经网络是一种基于误差反向传播算法的前馈神经网络,其结构如图2(a)所示,可被分为输入层、隐藏层与输出层,每层的节点数及隐藏层的数量可按需设置。本文所使用的BP神经网络输入层具备7个节点,隐藏层数量为2到5层,每一层均具备50个节点,输出层节点数为1。本文中LF处理时间、通电时间、通电量、吹氩时间、吹氩量、石灰加入量和钢水出站温度等7个参数通过输入层对应的7个节点输入神经网络后,在隐藏层的每个节点进行公式(1)所示的运算,数据通过连接线在节点上单向流动,直到在输出层节点上通过公式(1)得到预测值,上述步骤被称为正向传播。式中,o为隐藏层任意节点的输出值,如图2(a)中的节点N;n为前一层的节点数;wi代表前一层的第i个节点与当前节点之间的权重;bi代表当前节点的偏置;f为激活函数。正向传播目的是得到预测值,但无法提升预测值的精确度。本文按公式(2)将预测值与实际值进行比较得到误差,再将误差按公式(3)以链式求导法则反向传播到需要进行参数更新的节点上,以传播到该节点的误差按公式(4)进行参数更新。该步骤被称为参数更新,目的是使预测值更加准确。式中,E表示误差;t为真实值;o为神经网络的预测值。式中,t的值与权重w无关,又因为o的计算公式已知,因此可将公式(1)代入公式(3)中将误差逐层反向传递,直到误差传递至需要更新的参数处,偏置的误差计算方法与此相似。式中,wnew和wold分别代表已更新和未更新的权重,其中α是学习率,在本文中α的取值范围为0到1,该公式可代表梯度下降算法。此外,偏置的更新方法与权重相似。
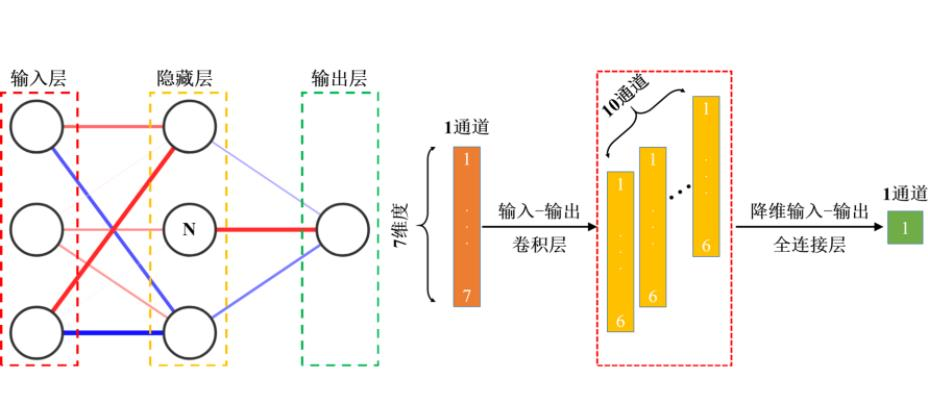
图2 本文使用的神经网络结构示意图
(a)BP神经网络结构示意图;(b)卷积神经网络数据结构示意图
1.2.2 卷积神经网络
卷积神经网络(CNN)是一种基于误差反向传播算法的前馈神经网络,其独特的卷积层结构使之具备优秀的特征提取功能。本文搭建的CNN由卷积层和全连接层组合而成,其中卷积层的数量可在有限范围内进行调整,全连接层数量可按需调整。本文设置的卷积层数量为3到5层,全连接层为1层,卷积核长为1×2和1×3,步幅为1,通道数设置为10到40。当LF处理时间等7个参数通过输入层进入到卷积层后,进行如图3所示的一维卷积,卷积核在输入的七维数据上移动,由于卷积核的维度为2,且移动步幅为1,卷积后输出数据维度为6,且卷积后数据通道数量与卷积核通道数量应该保持一致。卷积层输出的数据最终需以全连接层进行降维输出,目的是得到炉衬剩余厚度预测值。
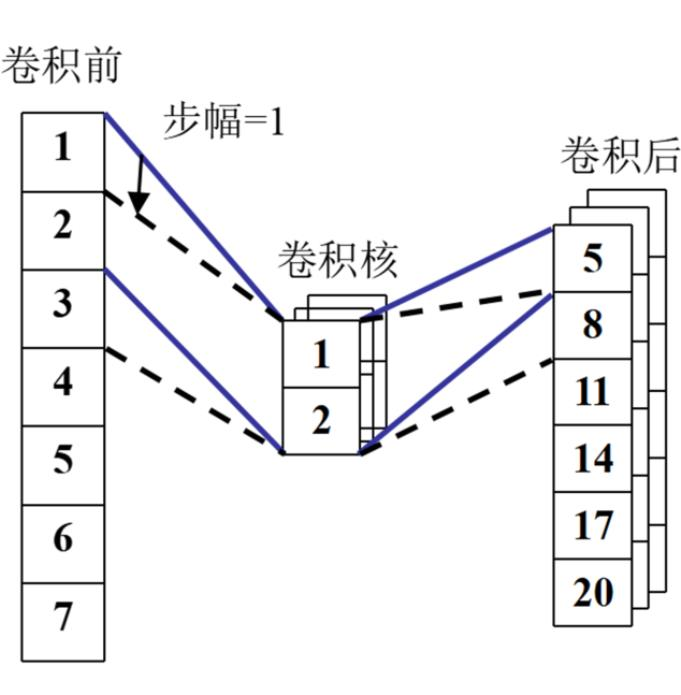
图3 一维卷积运算示意图
1.3 预测模型结构
由于单次大修期间LF精炼炉所记录的参数与炉衬剩余厚度测量值之间呈现出多对一的特点,本文按该特点修改了神经网络的参数更新时间,基于Python 3.9.7与PyTorch 1.9.1建立了如图4所示的预测模型。图中单个样本为一次LF精炼记录的7个参数,大修期间精炼n次,精炼数据构成n行7列的矩阵,按公式(5)对该矩阵进行归一化,目的是消除异常数据对结果的影响。将归一化后的矩阵输入神经网络后得到n行1列的输出,该输出中每一行代表神经网络预测的本次精炼造成的炉衬熔损厚度,而后将神经网络的输出值求和,再与标签数据进行比较计算误差,而后将误差反向传递至神经网络各层并更新参数,从而使预测值更加准确。待学习次数达到阈值后,神经网络跳出循环,进行反归一化得到预测的炉衬蚀损量。本文所使用的训练集为60张大修表,每张大修表具备160-260次精炼数据与一个磨损记录数据,测试集为20张大修表。每张大修表学习次数设置为300次,60张大修表共学习18000次。式中:Output为已归一化的值,Input为需要被归一化的值。train_min和train_max分别为训练集中的最小值和最大值,两值确定后不可修改。
1.4 预测值精准度评价标准
预测模型在训练集上学习完毕后需在测试集上测试以观察预测模型的准确性。本文采用的评价指标为均方差,计算公式如下:式中,i代表测试集中第i张大修表,由于本文使用的测试集具备20张大修表,则i最大取20,yp为预测模型预测的第i次大修期间的炉衬总蚀损量,yr为第i次大修期间真实的炉衬总蚀损量,MSE即均方差。由定义式可知,MSE越小,预测模型在测试集上的整体表现越好。
2. 结果与讨论
2.1 影响因素分析
在神经网络层数足够时,预测模型的预测能力与训练集中数据量存在较大相关性,但实际训练集的数量是有限的,如何在训练集有限的情况下得到预测精准度较高的预测模型是本文研究的重点。此部分主要从神经网络的层数、学习率取值、激活函数种类、神经网络类型这几方面进行探讨。在本次研究中,每一种网络层数、学习率、激活函数的搭配都重复了5次实验,以确保结果的可靠性。如图5(a)所示,在学习率固定时,神经网络层数的增加与5次实验中MSE小于50次数呈正相关,如在学习率为1E-05,激活函数与训练集数据保持不变,神经网络层数由二层增加到六层时,MSE小于50的次数由0次增加到5次,预测精度与稳定性得到了大幅提升。这是因为神经网络隐藏层节点的数量限制了其的预测能力的上限,在神经网络层数为二时,该网络仅有一个隐藏层,预测结果表明该网络难以捕捉数据中的规律。BP神经网络使用误差反向传播和梯度下降算法使MSE减小,学习率是控制梯度下降幅度的参数,其取值决定了MSE能否有效减少。图5(a)中,当神经网络层数控制在二到五层时,MSE随着学习率的减少而增大,这表明本研究中1E-06的学习率已过小,导致更新的参数值陷入某局部最优区域,导致过拟合。同时本文使用了隐藏层数为六、学习率为1E-05的BP神经网络来验证激活函数对预测模型的影响。以常见的Sigmoid、Tanh、Relu及其变种RRelu四个激活函数进行组合训练,结果如图5(b)所示,只有激活函数为全为Sigmoid或是Sigmoid与其它激活函数的组合时,预测模型才能较为准确地进行磨损预测。
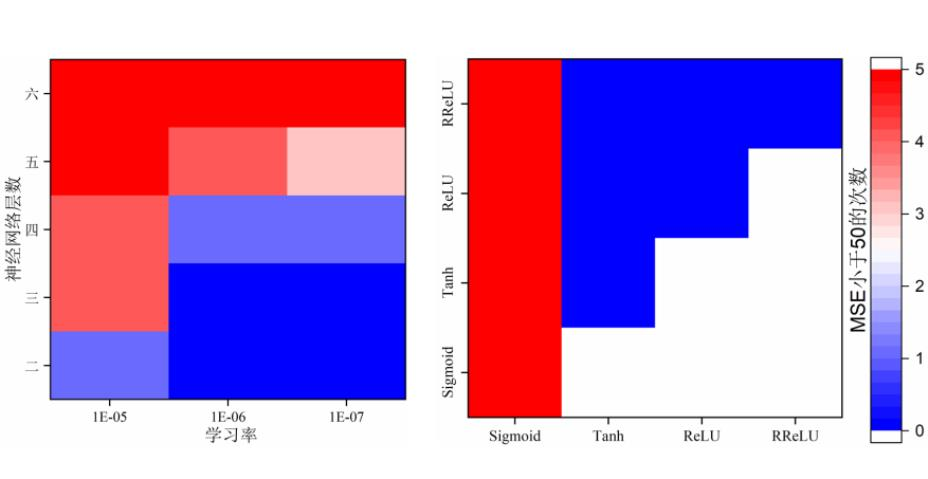
图5 不同参数对使用BP神经网络的预测模型的影响
(a)网络层数及学习率对预测模型的影响; (b)不同激活函数组合对预测模型的影响。
本文修改了卷积神经网络中卷积层数量、卷积层的通道数、学习率等参数,来判断神经网络类型的改变对预测模型表现的影响。本次实验中设置最小的卷积神经网络中卷积层数量为3,通道为10,学习率为1E-02,最大的卷积神经网络卷积层数量为6,通道为40,学习率为1E-01。使用CNN的预测模型在测试集上的MSE均在40到42的范围内,相比于使用BPNN的预测模型稳定性更高,但在相同训练集的情况下,基于CNN的最小结构的预测模型(卷积层数为3,每一层通道为10,激活函数为Sigmoid,学习率为1E-02)训练时间约为基于BP神经网络的最大规模预测模型(神经网络层数为六、激活函数为Sigmoid,学习率为1E-07)的三倍。
2.2 预测结果分析
预测模型在测试集上的整体表现如图6所示,图中MSE为34.15,出自层数为5,学习率为1E-06,激活函数为Sigmoid的BP神经网络,相比于MSE为43.15的情况,MSE为34.15时预测模型在测试集中样本7、8、14、16、18上表现地更加良好,图6(b)中MSE=34.15时预测模在测试集上平均误差为4.48%,MSE=43.15平均误差为5.08%。图6表示MSE可用于衡量预测模型结果的精确度,且本文建立预测模型能有效的预测磨损。
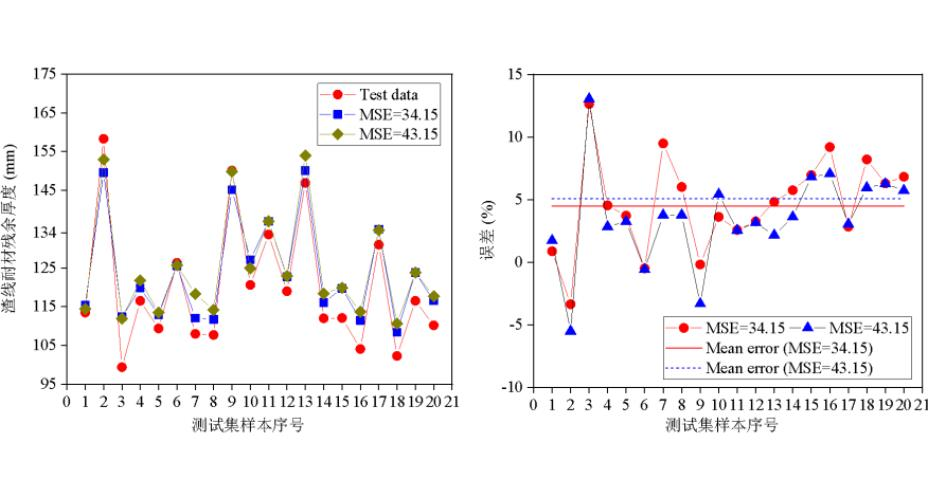
图6 预测模型在测试集上的表现结果
(a)测试集数据与预测数据对比;(b)测试集上误差分布。
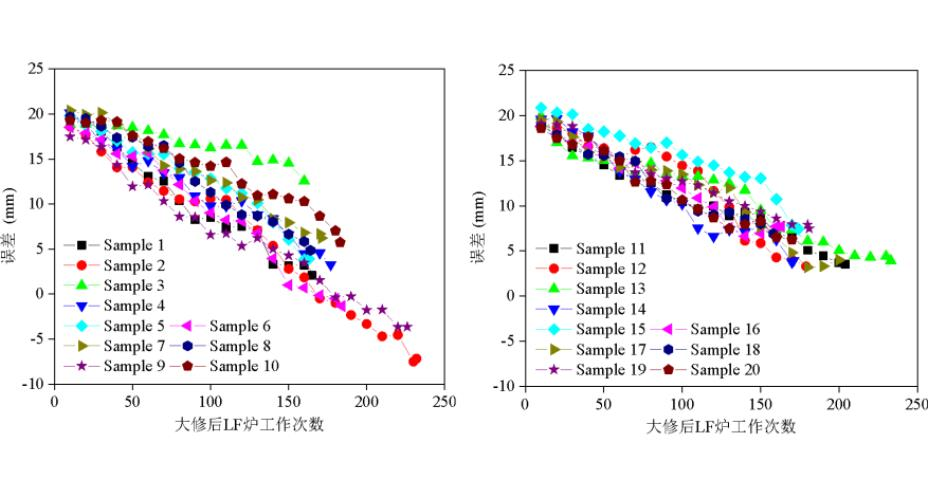
图7 单次大修期间预测模型的误差变化
(a)测试集1-10;(b)测试集11-20。
图7展示了大修期间预测模型预测误差随精炼次数的变化,在精炼次数较少时,预测模型预测的磨损误差较大,这是由反归一化导致的,可参考公式(5)的反公式。随着精炼次数的增加,预测模型的误差在逐渐降低,图7显示,在工作100炉后,测试集20个样本中有19个样本的预测误差在10 mm内。
2.3 结果应用建议
本文建立了钢包渣线处耐火材料剩余厚度预测模型,在1.1章节中通过分析精炼渣对镁碳砖的侵蚀机理,指出了影响耐材侵蚀的参数,而后将这些参数与现场记录参数取交集从而确定输入预测模型的参数。在应用时,预测模型的输入应当尽可能多的包含精炼渣的相关成分,如预熔渣成分,同时也应包含精炼渣的性能参数,如流动性,光学碱度等。由于不同公司生产的优势钢种不同,且钢包几何尺寸存在差异,导致钢包大修期间平均精炼次数不一,较少的平均80炉次[31],较多的平均200炉次,为了缩短数据的积累时间,在精炼钢包服役一定炉次后进行渣线处耐火材料剩余厚度的检测是必要的,且在应用本文提出的预测模型时,精炼流程中LF精炼应当占主导地位。
3 结论
(1)本文通过结合镁碳砖蚀损机理和现场数据特征,利用LF处理时间、通电时间、通电量、吹氩时间、吹氩量、石灰加入量和钢水出站温度7个工艺参数来训练神经网络,建立了LF精炼钢包炉衬蚀损预测模型。(2)使用BP神经网络时,网络层数控制在6层,激活函全为Sigmoid或Sigmoid与Tanh、ReLU及其变种组合时,预测模型在测试集上的稳定性较高,实验中MSE均小于50。且与BP神经网络相比,使用卷积神经网络时,预测模型对神经网络的层数、通道数、学习率等参数调整所要求的技巧更低,预测模型稳定性也较高,但训练卷积神经网络需要的时间是BP神经网络的3到5倍。(3)基于特定BP神经网络(三层全连接层,每层均为50个节点,激活函数为Sigmoid,学习率为1E-06)的预测模型在测试集上达到最小为34.15的MSE,在测试集上平均误差为4.48%。在单次大修期间,预测模型的误差随着工作炉次的增加而减小,在工作100炉次后,预测模型在95%的测试集上预测预测误差小于10 mm。
















